Signalons encore qu'on peut également représenter le nombre 4051 sous forme binaire dans un tableau, où on "coche" les puissances de 2 présentes:


TowerCorp.
www.helpmaths.net ←Nous sommes habitués à compter dans le système décimal, où chaque nombre est divisé en unités, dizaines, centaines,
milliers, et ainsi de suite, de la droite à la gauche, chaque chiffre composant ce nombre indiquant le nombre d'unités, de dizaines, de centaines,
etc. (c'est en fait un système de position). Par exemple, 4051 signifie 1 unité plus 5 dizaines plus 0 centaines plus 4 milliers. En fait,
cela équivaut à indiquer le nombre de chaque puissance de 10, de la droite à la gauche: si on reprend le nombre 4051, il équivaut à
1⋅100 + 5⋅101 + 0⋅102 + 4⋅103, soit 1 + 50 + 4000.
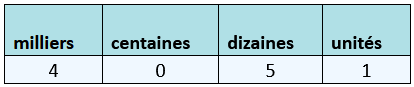
On peut le représenter sous forme de tableau:
Mais il existe un autre système de numération, utilisé dans le moindre appareil électronique: le système binaire. Ce système n'utilise que deux valeurs: "0" ou "1". Pourquoi? Parce qu'il est basé sur la caractéristique principale d'un circuit électrique: être parcouru ou non d'un courant électrique. Lorsque le courant passe, cela équivaut à "1"; quand aucun courant ne passe, cela équivaut à "0". De cette façon, on peut coder n'importe quel nombre, et surtout faire des calculs très rapidement.
Comme dans le système décimal, on codifie les nombres de droite à gauche dans le système binaire; mais contrairement au système décimal, qui utilise les puissances de 10, le système binaire utilise les puissances de 2.
Dans le système décimal, on indique pour un nombre donné de combien de chaque puissance de 10 il est composé (voir ci-dessus pour le nombre 4051). Dans le système binaire, on se contente de "cocher" chacune des puissances de 2 dont il est composé (c'est également un système de position), et de les additionner.
Reprenons le nombre 4051. la plus grande valeur issue d'une puissance de 2 comprise dans ce nombre est 2048 (211). Il reste donc 2003
(4051-2048). La plus grande valeur issue d'une puissance de 2 comprise dans 2003 est 1024 (210). Il reste donc 979. Et on continue:
979-512 (29) = 467; 467-256 (28) = 211; 211-128 (27) = 83; 83-64 (26) = 19; 19-16 (24) = 3;
3-2 (21) = 1; 1-1 (20) = 0. Il suffit maintenant, pour obtenir l'expression de 4051 en notation binaire, de mettre un "1" à
l'emplacement des puissances de 2 présentes et un "0" là où elles sont absentes, de droite à gauche; on obtient 111111010011. Vérifions:
20 + 21 + 24 + 26 + 27 + 28 + 29 + 210 + 211 =
1 + 2 + 16 + 64 + 128 + 256 + 512 + 1024 + 2048 = 4051.
Signalons encore qu'on peut également représenter le nombre 4051 sous forme binaire dans un tableau, où on "coche" les puissances de 2 présentes:

Nous ajouterons finalement qu'on peut effectuer les quatre opérations usuelles (addition, soustraction, multiplication, division) en utilisant les nombres binaires (c'est bien à cela qu'ils servent dans les machines à calculer et les ordinateurs!). Ceci sera le sujet d'un prochain "bonus"...