
TowerCorp.
www.helpmaths.net ←Il existe une méthode très simple pour mesurer la hauteur d'un arbre; la seule contrainte est de pouvoir le voir dans sa globalité depuis une certaine distance.
Prenez deux baguettes de même longueur — par exemples deux baguettes japonaises pour manger des sushis. Placez l'une des deux baguettes horizontalement à la base de votre nez, puis placez verticalement la deuxième baguette à l'extrémité de la première, à mi-hauteur. Vous obtenez ainsi une croix.
Maintenant, déplacez-vous de sorte que le bas de la baguette verticale coïncide avec la base du tronc de l'arbre et le haut de la baguette avec le sommet de l'arbre. La distance qui vous sépare de l'arbre correspond à sa hauteur!
Pour calculer cette distance, c'est très simple: chacun de vos grands pas correspond environ à une longueur de un mètre (vous pouvez mesurer pour vérifier). Le nombre de pas entre vous et l'arbre correspond alors à la distance qui vous en sépare en mètres...
Le secret de la méthode réside dans le théorème de Thalès(1).
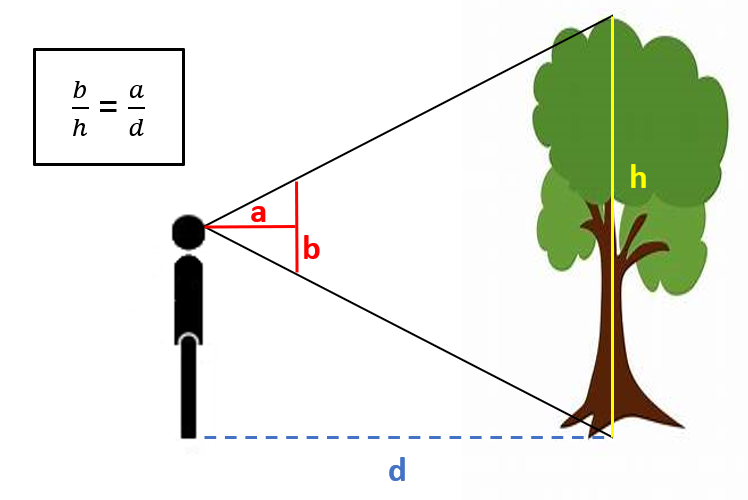
Figure 1: Illustration de la méthode du bûcheron.
Sur la Figure 1, on voit deux triangles: un grand triangle de base h et un petit triangle de base b (les deux bases doivent impérativement être parallèles, sinon le théorème ne marche pas). Ces deux triangles sont semblables, c'est-à-dire qu'ils ont les mêmes proportions. Le théorème de Thalès nous dit que a/b = d/h. Mais ici, a = b, donc a/b = 1. On peut donc récrire l'équation ainsi: a/b = 1. Et donc, en remaniant l'équation, on obtient finalement... d = h! Donc la distance de l'observateur à l'arbre est égale à sa hauteur... CQFD!