
TowerCorp.
www.helpmaths.net ←On a tous un jour entendu le mot "fractal" ou "fractale"; mais sait-on à quoi cela correspond? En fait, "fractal" est dérivé de "fraction "". Et un objet fractal, c'est un objet qui a une dimension... fractionnaire, c'est-à-dire qu'il n'est ni de dimension 1 (une droite ou une courbe), ni de dimension 2 (une surface), ni de dimension 3 (un volume), mais par exemple de dimension... 1,26. Encore un délire de mathématiciens sans aucun rapport avec le monde réel ? Voire...
Une autre façon peut-être plus compréhensible de définir un objet fractal, c'est de dire que quelle que soit l'échelle à laquelle on l'observe, c'est-à-dire globalement dans son ensemble ou au contraire fortement grossi, on ne constatera quasiment aucune différence. En d'autres termes, un objet fractal apparaît identique à lui-même qu'on l'observe dans son entier ou qu'on zoome fortement! Et là, on peut donner des exemples concrets dans le monde réel. Un nuage, par exemple: sa forme est quasiment identique qu'on le regarde en détail ou en entier. Ou une côte rocheuse : qu'on la regarde d'avion ou directement du sol, elle sera toujours découpée plus ou moins irrégulièrement! Ou un système de cours d'eau. Ou les branches d'un arbre. Ou l'embranchement des bronches et des bronchioles dans les poumons. Le plus bel exemple est peut-être le chou Romanesco (figure 1): sur au moins trois ordres de grandeur, il reproduit sa forme exactement identique à elle-même, de façon si parfaite qu'on le croirait fabriqué artificiellement...

Figure 1: chou Romanesco(Source: jardinerfacile.fr)
Pour expliquer mathématiquement ce qu'est un fractal, nous prendrons un exemple classique : le flocon de Koch.
Prenons un segment de droite composé de trois unités. Ajoutons-lui un segment de longueur une unité. Puisqu'on passe d'un segment de longueur 3 à un segment de longueur 4, on multiplie la longueur originale par 4/3. Prenons maintenant notre figure composée de 4 segments, et opérons sur chacun de ces segments la même transformation que celle opérée sur le segment initial. On obtient alors une figure à 16 segments, de longueur totale 16/3. Répétons encore une fois l'opération: on obtient une figure à 64 segments, de longueur 64/9. A chaque étape, le nombre de segments est donc multiplié par 4, et la longueur de la figure augmente d'un facteur 4/3 (voir figure 2).
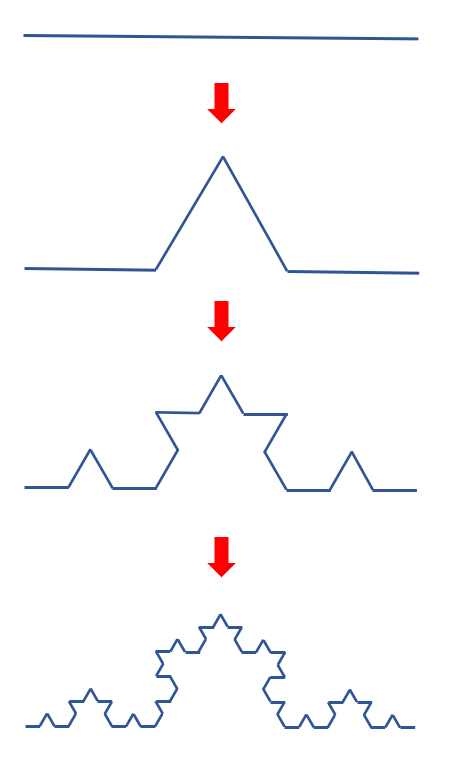
Figure 2 : les trois premières transformations pour obtenir le flocon de Koch.
Ce qui est intéressant, c'est qu'on passe d'une figure originale de longueur finie à une figure finale ayant une longueur... infinie! Et pourtant, cette figure finale de longueur infinie n'occupe qu'une partie finie de l'espace (et la longueur de sa base mesure toujours... trois unités). Ce qui est particulier, c'est qu'elle n'occupe plus seulement une seule dimension comme la figure initiale (un segment de droite), mais elle n'occupe pas non plus totalement la seconde dimension (le plan); elle se trouve... entre les deux, dans une dimension donc fractionnaire!.
Pour en revenir à notre flocon de Koch, on l'obtient "simplement" en opérant les transformations décrites précédemment non pas sur un seul segment, mais sur les trois côtés d'un triangle équilatéral (figure 3).

Figure 3 : le flocon de Koch après trois transformations du triangle équilatéral de base.
Pour calculer la dimension de notre figure finale (ou celle du flocon de Koch, qui en dérive), il suffit de diviser le logarithme (naturel ou non) de la longueur après la première transformation par le logarithme (naturel ou non) de la longueur avant la première transformation. Dans le cas de notre figure, sa dimension est donc de ln(4)/ln(3) ≈ 1,26, c'est-à-dire effectivement entre 1 et 2!
Avec sa dimension de 1.26, le flocon de Koch est bien un objet fractal...