
TowerCorp.
www.helpmaths.net ←Les huit(1) planètes du système solaire tournent autour du Soleil en suivant des orbites stables, dans l'ordre suivant en termes d'éloignement à notre étoile : Mercure, Vénus, la Terre, Mars, Jupiter, Saturne, Uranus et Neptune. Puisque leurs orbites sont stables, leurs distances moyennes(2) au Soleil sont bien établies.
Et là, surprise : on trouve une suite mathématique (encore une!) qui donne une très bonne estimation de la distance D des planètes au Soleil jusqu'à Uranus, en termes de nombre d'unités astronomiques (UA), l'unité astronomique étant la distance de la Terre au Soleil, à savoir 150 millions de kilomètres du Soleil en moyenne.
Cette série suit la formule suivante : D = (3×2n + 4)/10, avec n allant de –∞ (Mercure) à 6 (Uranus). Dans le tableau 1, nous donnons les valeurs D obtenues par calcul, et les distances moyennes réelles au Soleil. En multipliant les valeurs de D par 150'000'000 (ou 1.5×108), on obtient des valeurs (en kilomètres) remarquablement similaires aux valeurs réelles...
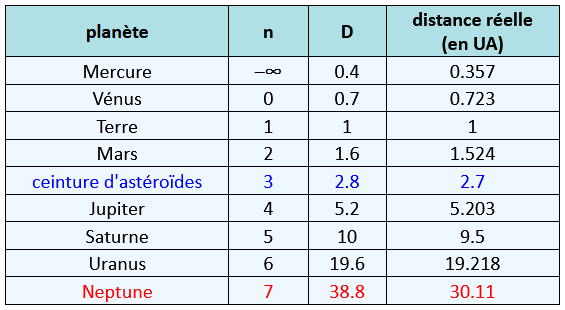
Tableau 1: distances des planètes au Soleil (en UA).
En regardant le tableau 1, on constate trois choses. Tout d'abord, l'accord est remarquablement bon pour toutes les valeurs, sauf pour Neptune (nous y reviendrons plus loin). Ensuite, on voit que la valeur de 2.7 apparaît entre Mars et Jupiter, là où il n'y a aucune planète. Aucune planète, certes... mais cet emplacement n'est pas vide: c'est en effet là que se trouve la ceinture d'astéroïdes(3)! Notre suite a donc une valeur prédictive... Enfin, la valeur pour Neptune ne correspond pas, probablement parce que cette planète a subi une collision avec un autre corps de grande taille(4) qui a modifié son orbite.
Alors, hasard ou loi de la Nature?