1.618(etc.), un nombre magnifique

Commençons par donner une simple équation: f(x) = x² – x – 1 = 0. (1)

Une équation froide, brute, sans signification aucune apparente. Et pourtant… la beauté du monde s’y cache.

le nombre Φ

Toute personne ayant un minimum de souvenirs en mathématiques se rappelle qu’une équation comportant un terme en x² est l’équation d’une parabole.

La Figure 1 donne l’illustration de l’équation (1).

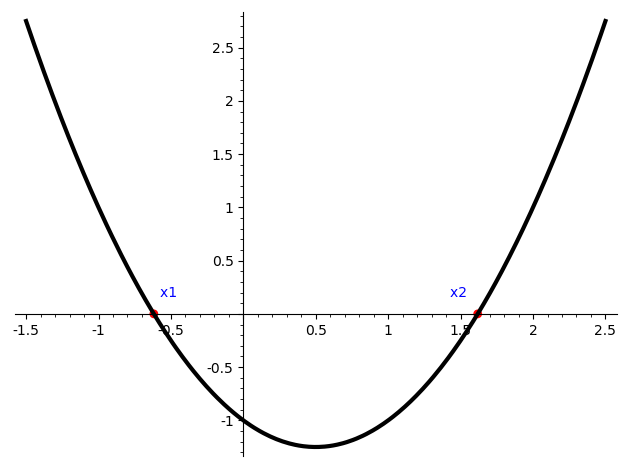
Figure 1 : graphique de l’équation f(x) = x² – x – 1 = 0.

En regardant la figure, on constate que la courbe croise l’axe des x(1) en deux points. Un calcul simple(2) permet de trouver les coordonnées de ces deux points. La première est négative (x1 ≃ –0,618): elle peut être mise de côté, elle n’a pas d’utilité pour la suite de ce qui nous intéresse. En revanche, x₂ est au cœur du mystère...

La valeur décimale de x₂ est égale à environ 1,618. Environ seulement, parce que tout comme π ou encore √2, ce nombre est un irrationnel, c’est-à-dire que ses décimales se poursuivent à l’infini sans jamais se répéter(3).

Le nombre 1,618… est ce qu’on appelle le nombre d’or, symbolisé par la lettre grecque Φ (« phi »). Des bibliothèques entières ont été écrites à son propos ; nous nous contenterons de mentionner qu’il est aussi appelé la divine proportion et qu’il est à l’origine de la sensation de beauté conférée par nombre d’oeuvres d’art dont les proportions respectent ce « nombre d’or ». Mais il est loin de ne s’appliquer qu’aux créations humaines, comme nous allons le voir…

Un exemple dans le règne animal

Maintenant, un peu de géométrie. Pour expliquer plus précisément à quoi correspond Φ, construisons un rectangle selon la procédure suivante: construisons un carré ABCD, et prolongeons sa base AB sur la droite (Figure 2). Plantons la pointe d’un compas au centre (O) de sa base, plaçons sa mine sur le coin supérieur droit (C) du carré, et traçons un arc de cercle jusqu’à la prolongation de la base du carré ; nous obtenons le point E. Finalement, plaçons le point F sur une droite verticale passant par le point E, à l’extrémité d’un segment de la même longueur que le segment AB. Nous obtenons ainsi le rectangle AEFD, qu’on peut diviser en un carré ABCD et un rectangle BEFC (Figure 2).

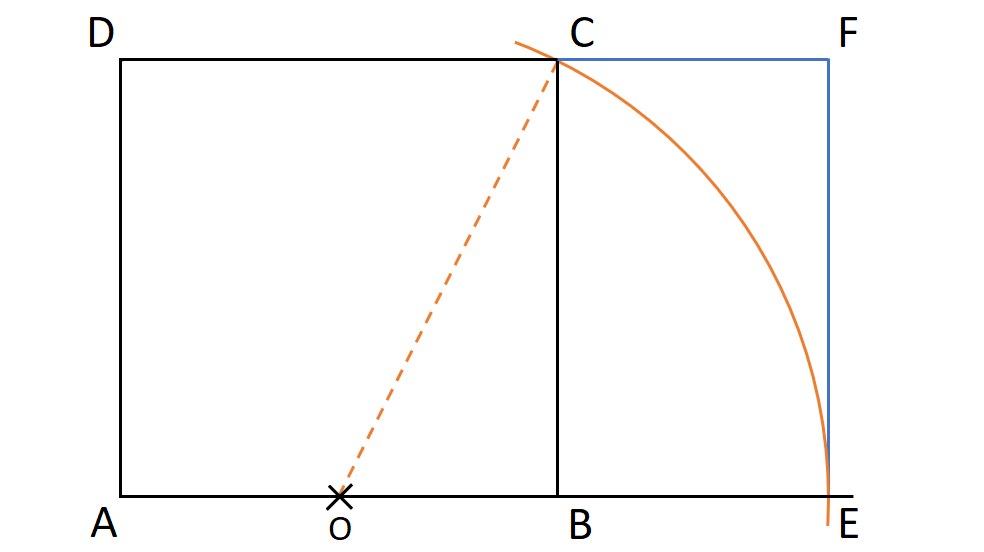
Figure 2: Rectangles d'or AEFD et BEFC.

Le rectangle ABCD a une propriété très particulière : le rapport entre la longueur de son long côté AE et celle de son petit côté AD (ou AB) d’une part, et le rapport de son petit côté AD (ou AB) avec le segment correspondant à la longueur du grand côté moins celle du petit côté (AE – AB = AE – AD, soit le segment BE) d'autre part, sont… identiques (et ils sont égaux à... Φ)! En d’autres termes, AE/AB = AB/BE. Autrement dit, les rectangles AEFD et BEFC sont semblables, c’est-à-dire qu’ils ont les mêmes proportions.

Maintenant, allons plus loin : divisons le rectangle BEFC en un carré et un rectangle. Ce dernier rectangle aura encore les mêmes proportions que les rectangles AEFD et BEFC ! Et on peut continuer ainsi à l’infini (Figure 3)…

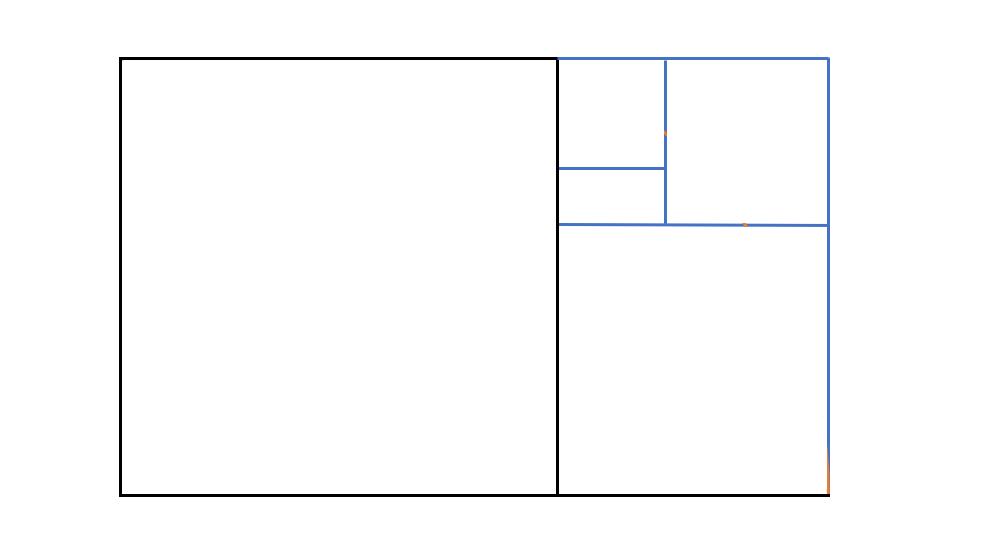
Figure 3: subdivision en rectangles d'or de plus en plus petits.

Et c’est là que les choses deviennent étonnantes : la nature utilise cette succession de rectangles semblables pour construire des formes qu’on retrouve chez certains organismes vivants. La figure 4 montre la spirale construite sur la suite de rectangles d’or construits selon la procédure précédente. Et c’est exactement la forme de la coquille d’un nautile (figure 5)…

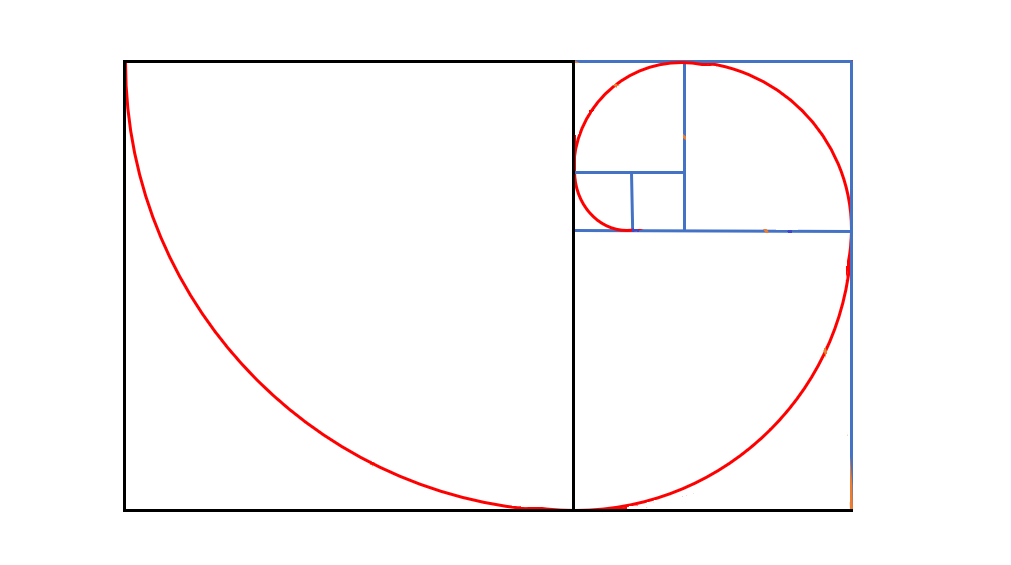
Figure 4: spirale construite sur la suite des rectangles d'or.

Figure 5: coupe d'une coquille de nautile (Nautilus pompilius)(Source: Fotosearch)

Magnifique, non ?

Mathématiques et botanique

Mais les choses ne s’arrêtent pas là. Il existe une suite mathématique particulière, la suite de Fibonacci(4), construite de la manière suivante: les deux premières valeurs sont 0 et 1; chacune des valeurs suivantes est la somme des deux précédentes. On obtient donc la suite:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

Et ce qui est étonnant dans cette suite, c’est que le rapport entre une valeur et la valeur précédente, lorsqu’on prend des paires de valeurs de plus en plus grandes, se rapproche de la valeur limite 1.618, soit, nous vous le donnons en mille… Φ. Et ce qui est extraordinaire, c’est que les valeurs de la suite de Fibonacci régissent certaines règles dans le règne végétal.

Tout d’abord, le nombre de pétales de n’importe quelle fleur est toujours un multiple d’un des nombres de Fibonacci. Ainsi, vous ne trouverez jamais de fleur ayant par exemple 17 pétales ; en revanche, les fleurs à 5 pétales (comme par exemple les roses sauvages ou les boutons d’or) sont extrêmement fréquentes, et le nombre de pétales d’une marguerite est souvent 21. Encore plus fort : le nombre de spires d’une pomme de pin ou celui du cœur d’une fleur de tournesol est toujours un nombre de Fibonacci, qu’on les compte dans un sens ou dans l’autre (Figure 6). Et il y a encore beaucoup d'autres exemples!

Figure 6: Spirales sur une pomme de pin. On retrouve les nombres de Fibonacci 13 et 8. (Source: cambridgeplanet.wordpress.com)

Pour reprendre les mots de Galilée(5), "la nature est écrite en langage mathématique"…

retour